Fractals are intricate geometric shapes that can be split into parts, each resembling the whole—a property known as self-similarity. These fascinating structures appear in various natural phenomena and have applications across multiple scientific disciplines. This article delves into three notable fractal curves: the Peano curve, the Hilbert curve, and the Koch curve, exploring their mathematical foundations, unique properties, and practical applications.
The Peano Curve: A Pioneer in Space-Filling

In 1890, Italian mathematician Giuseppe Peano introduced the Peano curve, marking the first discovery of a space-filling curve. This continuous curve traverses every point within a unit square, effectively mapping a one-dimensional line onto a two-dimensional plane. Constructed through an iterative process, each stage divides the square into smaller sections, with the curve weaving through each subdivision.
The Peano curve challenges traditional notions of dimensionality, demonstrating that a line can completely fill a plane area. This concept has profound implications in fields like topology and mathematical analysis, particularly in understanding the behavior of continuous functions and the structure of space.
The Hilbert Curve: An Elegant Space-Filling Fractal

Building upon Peano’s work, German mathematician David Hilbert introduced the Hilbert curve in 1891. This continuous fractal also fills a unit square but follows a distinct, more symmetrical pattern. The Hilbert curve is generated through an iterative process where each step refines the curve’s path, increasing its complexity while maintaining self-similarity.
The Hilbert curve’s orderly structure makes it valuable in computer science, especially in optimizing data storage and retrieval. Its ability to preserve spatial locality ensures that points close in multi-dimensional space remain close in the one-dimensional representation, enhancing the efficiency of algorithms in image processing and database indexing.
The Koch Curve: A Gateway to Infinite Perimeters
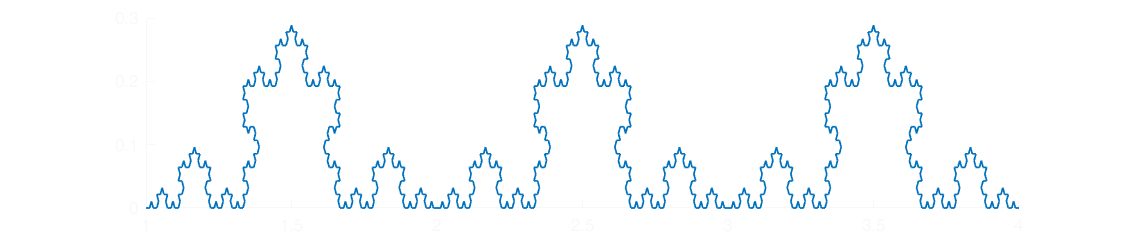
Swedish mathematician Helge von Koch introduced the Koch curve in 1904, offering a simple yet profound example of a fractal curve. Starting with a straight line segment, the construction involves dividing the segment into three equal parts, replacing the middle segment with two sides of an equilateral triangle, and repeating this process indefinitely.
The Koch curve exemplifies how a finite area can encompass an infinitely long perimeter. Each iteration increases the curve’s length by a factor of four-thirds, leading to an infinite perimeter as the process continues. This paradoxical property has applications in modeling natural phenomena with intricate boundaries, such as coastlines and snowflakes, where traditional Euclidean geometry falls short.
Fractals in Nature and Technology
Beyond theoretical mathematics, fractal curves like the Peano, Hilbert, and Koch curves have practical applications in modeling complex structures and phenomena. In nature, fractal patterns describe the irregular yet self-similar shapes of mountains, clouds, and biological systems. Technologically, fractals inform antenna design, enabling compact structures that efficiently transmit and receive signals across multiple frequencies.
In computer graphics, fractal algorithms generate realistic landscapes and textures by mimicking the self-similar patterns found in nature. Additionally, fractal geometry aids in understanding chaotic systems, where small changes in initial conditions can lead to vastly different outcomes, a concept relevant in fields like meteorology and finance.
Conclusion
The exploration of fractal curves such as the Peano, Hilbert, and Koch curves reveals the intricate relationship between mathematics and the natural world. These curves not only challenge our understanding of dimensions and geometry but also provide practical tools for modeling complex systems and structures. As research in fractal geometry advances, its applications continue to expand, influencing diverse fields from art and design to science and engineering.

Leave a Reply